Rich, thank you for the explanation.
I think it would be preferable to keep the more compact terms in the COM code, rather than expanding everything to a very long _expression_. If I understand correctly, this could be done with a few additional lines of code using temporary variable assignments.
I recognize that symbolic math manipulation requires a separate license, but anonymous functions do not.
Please consider if that can be done.
</Adee>
From: Norman Swenson <norm.swenson@xxxxxxxx>
Sent: Saturday, July 19, 2025 9:17 PM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
Thanks, Rich.
In my last bullet of https://www.ieee802.org/3/dj/public/25_07/swenson_3dj_01_2507.pdf , I said “This result [meaning that the reflection coefficient does not depend on the Z0 chosen as the reference impedance] holds for an arbitrary two-port network.” I computed the reflection coefficient for an arbitrary S-matrix, Z_source, and Z_load using Mathematica. I did not present the equation because it was so messy. I think you did the same thing using the matlab symbolic editor. When I get time, I will compare the two results to make sure we got the same answer.
Regards,
Norm
From: Richard Mellitz <Richard.Mellitz@xxxxxxxxxx>
Sent: Saturday, July 19, 2025 8:27 AM
To: norm.swenson@xxxxxxxx; STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: RE: [802.3_COM] Correction: Question about equation in function get_TDR
The function was created with the matlab symbolic editor. Not sure how much will show in email, but Hansel has is right.
S = sym('s%d%d',[2 2],'positive')
I=eye(2)
Z0in = sym('Z0in%d',[1 2],'positive')
Z0out = sym('Z0out%d',[1 2],'positive')
RHO =@(zin,zout) (zout-zin)./(zout+zin)
R=RHO(Z0in,Z0out).*I
amp =@(zin,zout) sqrt(zout./zin).*(1./(zout+zin))
A=amp(Z0in,Z0out).*I
SOUT=simplifyFraction( A^-1* (S-R) *(I-R*S)^-1 *A);
%Looking for TDR input port oof a s2p
syms Zin Zout
SOUT=subs(SOUT,Z0in(1),Zin);
SOUT=subs(SOUT,Z0in(2),Zin);
SOUT=subs(SOUT,Z0out(1),Zout);
SOUT=subs(SOUT,Z0out(2),Zout)
RL=simplify(SOUT(1,1))
collect(RL,[Zin,Zout])
TDR_RL=matlabFunction(RL)
S =
![]()
I = 2×2
1 0
0 1
Z0in =
![]()
Z0out =
![]()
RHO = function_handle with value:
@(zin,zout)(zout-zin)./(zout+zin)
R =

amp = function_handle with value:
@(zin,zout)sqrt(zout./zin).*(1./(zout+zin))
A =
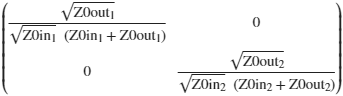
SOUT =

RL =
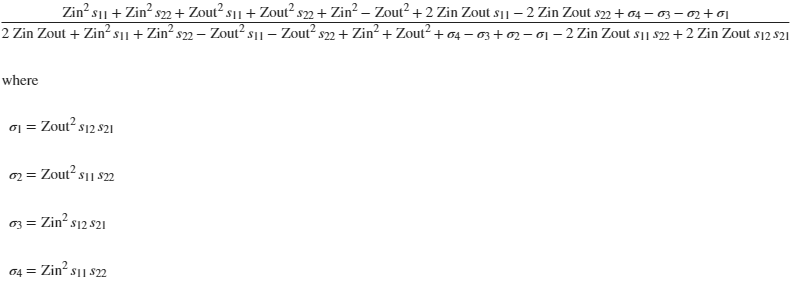
ans =
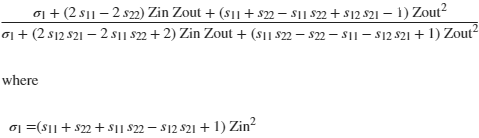
TDR_RL = function_handle with value:
@(Zin,Zout,s11,s12,s21,s22)(Zin.^2.*s11+Zin.^2.*s22+Zout.^2.*s11+Zout.^2.*s22+Zin.^2-Zout.^2+Zin.*Zout.*s11.*2.0-Zin.*Zout.*s22.*2.0+Zin.^2.*s11.*s22-Zin.^2.*s12.*s21-Zout.^2.*s11.*s22+Zout.^2.*s12.*s21)./(Zin.*Zout.*2.0+Zin.^2.*s11+Zin.^2.*s22-Zout.^2.*s11-Zout.^2.*s22+Zin.^2+Zout.^2+Zin.^2.*s11.*s22-Zin.^2.*s12.*s21+Zout.^2.*s11.*s22-Zout.^2.*s12.*s21-Zin.*Zout.*s11.*s22.*2.0+Zin.*Zout.*s12.*s21.*2.0)
|
From: Norman Swenson <norm.swenson@xxxxxxxx>
Sent: Saturday, July 19, 2025 6:09 AM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
Caution: This email originated from outside the organization. Do not click links or open attachments unless you recognize the sender and know the content is safe. |
Hansel
Thank you very much. I will study the presentation. I do believe it is what I thought it was based on your note below.
Regards,
Norm
From: Hansel DSilva <Hansel.D'Silva@xxxxxxxxxxxxxxxx>
Sent: Friday, July 18, 2025 10:53 PM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx; norm.swenson@xxxxxxxx
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
Hi Norman,
The function on line 63 of TDR_RL is the renormalized return loss (Sdd11' or Sdd22') where one is changing the differential reference impedance from sdd.Impedance to (2*ZT). Does this help answer the quesiton?
The function TDR_RL on line 63 is called by the following on line 71.
RL(i)=TDR_RL(sdd.Impedance,2*ZT,sdd.Parameters(param.RL_sel,param.RL_sel,i) ,sdd.Parameters( 1,2 ,i), sdd.Parameters( 2,1 ,i),sdd.Parameters( other_port,other_port ,i) );
Attached is a presentation that derives the formula on line 63, starting from the renormalization of a 2×2 S-matrix. It leads to an _expression_ for the renormalized return loss in terms of the original (unrenormalized) S-parameters and the input/output reference impedances.
Regards,
Hansel D'Silva
From: Norman Swenson <norm.swenson@xxxxxxxx>
Sent: Saturday, July 19, 2025 11:10 AM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx <STDS-802-3-COM@xxxxxxxxxxxxxxxxx>
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
CAUTION: EXTERNAL EMAIL
Correction: The name of the function (and corresponding .m file) is get_TDR.
From: norm.swenson@xxxxxxxx <norm.swenson@xxxxxxxx>
Sent: Friday, July 18, 2025 10:30 PM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: Question about equation in function TDR_results
Hello all
I am trying to reverse engineer the current version of COM in the main
branch. Lines 62 and 63 of the function get_TDR define a pure function:
% re-normalize reference of s-parameterss: this seems correct for a s4p
input file [sic]
TDR_RL
=@(Zin,Zout,s11,s12,s21,s22)(Zin.^2.*s11+Zin.^2.*s22+Zout.^2.*s11+Zout.^2.*s
22+Zin.^2-Zout.^2
<mailto:=@(Zin,Zout,s11,s12,s21,s22)(Zin.%5e2.*s11+Zin.%5e2.*s22+Zout.%5e2.*
s11+Zout.%5e2.*s22+Zin.%5e2-Zout.%5e2> +
Zin.*Zout.*s11.*2.0-Zin.*Zout.*s22.*2.0+Zin.^2.*s11.*s22-Zin.^2.*s12.*s21-Zo
ut.^2.*s11.*s22+Zout.^2.*s12.*s21)./(Zin.*Zout.*2.0+Zin.^2.*s11+Zin.^2.*s22-
Zout.^2.*s11-Zout.^2.*s22+Zin.^2+Zout.^2+Zin.^2.*s11.*s22-Zin.^2.*s12.*s21+Z
out.^2.*s11.*s22-Zout.^2.*s12.*s21-Zin.*Zout.*s11.*s22.*2.0+Zin.*Zout.*s12.*
s21.*2.0);
In typeset form, TDR_RL is given by :
Or, expressing the numerator and denominator as polynomials in Zin and Zout,
TDR_RL is:
I am wondering what this is. Is this an _expression_ of the return loss when
Zin and Zout are the source and load impedances, respectively, when they
differ from the reference impedance Z0 used to calculate the s-parameters?
(If so, this would be along the lines of the presentation I made last Monday
to the interim working group meeting, but I would like to be sure.)
Thanks for any guidance anyone can provide.
Regards,
Norm
________________________________________________________________________
To unsubscribe from the STDS-802-3-COM list, click the following link: https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1
________________________________________________________________________
THIS EMAIL ORIGINATED FROM AN EXTERNAL SOURCE (outside of Amphenol-TCS),
PLEASE USE CAUTION WHEN EVALUATING ITS CONTENTS.
This e-mail has been scanned by MCI Managed Email Content Service, using Skeptic(tm)
technology powered by MessageLabs. To report SPAM or other related email issues please
send an email to Postmaster@xxxxxxxxxxxxxxxx
________________________________________________________________________
To unsubscribe from the STDS-802-3-COM list, click the following link: https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1
To unsubscribe from the STDS-802-3-COM list, click the following link: https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1
To unsubscribe from the STDS-802-3-COM list, click the following link: https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1