I think
TDR_RL was added toward the end of .3ck (~2020). Adam Gregory made a relatively recent addition for .3dj, read_Nport_touchstone.m. Port renormalization was included here. Making that part code for renormalization
as a subfunction could be helpful.
There are a lot of clean up should happen. It just a question of priorities.
I’d like to see where we end up with in d2.1 to keep syntax aligned before doing this.
Norm seemed to suggest that impedances should be clearly defined.
Here’s a tabulation of what I have
-
Source impedance
-
Load impedance
-
s-parameter touchstone reference impedance
-
Internal computational reference impedance
-
Reference mpedance used for s-parameter graphs
-
Impedance of s-parameter used for FD computations (like for the test fixtures)
-
Physical characteristic impedance
The naming syntax and context for the above is not consistent in the evolutionary COM code.
… Rich
|
From: Adam Gregory <000046be97a4acdb-dmarc-request@xxxxxxxxxxxxxxxxx>
Sent: Monday, July 21, 2025 8:30 AM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
|
Caution: This email originated from outside the organization. Do not click links or open attachments unless you recognize the sender and know the content is safe.
|
I agree that simplifying the _expression_ so that it is not one large equation is preferred.
There is a proposal to add a per-port renormalization function to COM. This would make that section much more readable. In addition to using it in get_TDR.m, a renormalization function could also be applied
to this block of s21_pkg.m where the Tx and Rx die termination are added:
if include_die
s21p= H_t.*s21.*(1-gamma_tx).*(1+gamma_rx)./(1.- s11.*gamma_tx - s22.*gamma_rx -s21.*s12.*gamma_tx.*gamma_rx +s11.*s22.*gamma_tx.*gamma_rx);
else
s21p=s21; % if no die we do not want a VTF
end
Thanks,
Adam
|
From: Adee Ran (aran) <0000147b29386f6c-dmarc-request@xxxxxxxxxxxxxxxxx>
Sent: Sunday, July 20, 2025 5:49 AM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
Rich, thank you for the explanation.
I think it would be preferable to keep the more compact terms in the COM code, rather than expanding everything to a very long _expression_. If I understand correctly,
this could be done with a few additional lines of code using temporary variable assignments.
I recognize that symbolic math manipulation requires a separate license, but anonymous functions do not.
Please consider if that can be done.
</Adee>
From: Norman Swenson <norm.swenson@xxxxxxxx>
Sent: Saturday, July 19, 2025 9:17 PM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
Thanks, Rich.
In my last bullet of
https://www.ieee802.org/3/dj/public/25_07/swenson_3dj_01_2507.pdf , I said “This result [meaning that the reflection coefficient does not depend on the Z0 chosen as the reference impedance] holds for an arbitrary two-port network.” I computed the reflection
coefficient for an arbitrary S-matrix, Z_source, and Z_load using Mathematica. I did not present the equation because it was so messy. I think you did the same thing using the matlab symbolic editor. When I get time, I will compare the two results to make
sure we got the same answer.
Regards,
Norm
From: Richard Mellitz <Richard.Mellitz@xxxxxxxxxx>
Sent: Saturday, July 19, 2025 8:27 AM
To: norm.swenson@xxxxxxxx;
STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: RE: [802.3_COM] Correction: Question about equation in function get_TDR
The function was created with the matlab symbolic editor. Not sure how much will show in email, but Hansel has is right.
S = sym('s%d%d',[2
2],'positive')
I=eye(2)
Z0in = sym('Z0in%d',[1
2],'positive')
Z0out = sym('Z0out%d',[1
2],'positive')
RHO =@(zin,zout) (zout-zin)./(zout+zin)
R=RHO(Z0in,Z0out).*I
amp =@(zin,zout) sqrt(zout./zin).*(1./(zout+zin))
A=amp(Z0in,Z0out).*I
SOUT=simplifyFraction( A^-1* (S-R) *(I-R*S)^-1 *A);
%Looking for TDR input port oof a s2p
syms
Zin Zout
SOUT=subs(SOUT,Z0in(1),Zin);
SOUT=subs(SOUT,Z0in(2),Zin);
SOUT=subs(SOUT,Z0out(1),Zout);
SOUT=subs(SOUT,Z0out(2),Zout)
RL=simplify(SOUT(1,1))
collect(RL,[Zin,Zout])
TDR_RL=matlabFunction(RL)
S =
![]()
I = 2×2
1 0
0 1
Z0in =
![]()
Z0out =
![]()
RHO = function_handle with value:
@(zin,zout)(zout-zin)./(zout+zin)
R =

amp = function_handle with value:
@(zin,zout)sqrt(zout./zin).*(1./(zout+zin))
A =
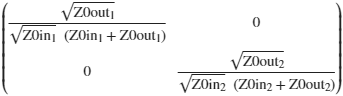
SOUT =

RL =
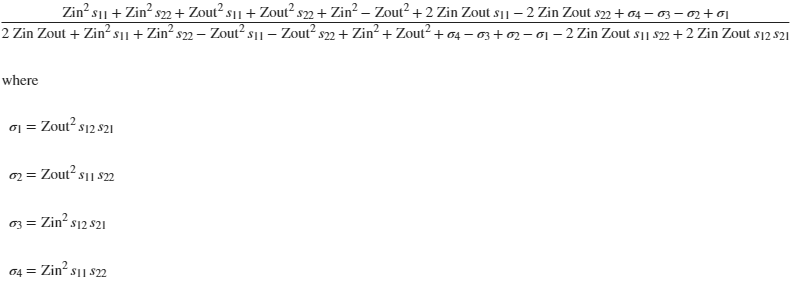
ans =
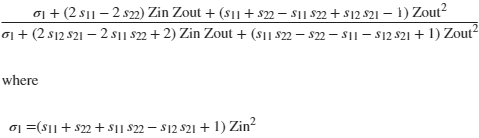
TDR_RL = function_handle with value:
@(Zin,Zout,s11,s12,s21,s22)(Zin.^2.*s11+Zin.^2.*s22+Zout.^2.*s11+Zout.^2.*s22+Zin.^2-Zout.^2+Zin.*Zout.*s11.*2.0-Zin.*Zout.*s22.*2.0+Zin.^2.*s11.*s22-Zin.^2.*s12.*s21-Zout.^2.*s11.*s22+Zout.^2.*s12.*s21)./(Zin.*Zout.*2.0+Zin.^2.*s11+Zin.^2.*s22-Zout.^2.*s11-Zout.^2.*s22+Zin.^2+Zout.^2+Zin.^2.*s11.*s22-Zin.^2.*s12.*s21+Zout.^2.*s11.*s22-Zout.^2.*s12.*s21-Zin.*Zout.*s11.*s22.*2.0+Zin.*Zout.*s12.*s21.*2.0)
|
From: Norman Swenson <norm.swenson@xxxxxxxx>
Sent: Saturday, July 19, 2025 6:09 AM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
|
Caution: This email originated from outside the organization. Do not click links or open attachments unless you recognize the sender and know the content is safe.
|
Hansel
Thank you very much. I will study the presentation. I do believe it is what I thought it was based on your note below.
Regards,
Norm
From: Hansel DSilva <Hansel.D'Silva@xxxxxxxxxxxxxxxx>
Sent: Friday, July 18, 2025 10:53 PM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx;
norm.swenson@xxxxxxxx
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
Hi Norman,
The function on line 63 of TDR_RL is the renormalized return loss (Sdd11' or Sdd22') where one is changing the differential reference impedance from sdd.Impedance to (2*ZT). Does this help answer the quesiton?
The function TDR_RL on line 63 is called by the following on line 71.
RL(i)=TDR_RL(sdd.Impedance,2*ZT,sdd.Parameters(param.RL_sel,param.RL_sel,i) ,sdd.Parameters( 1,2 ,i), sdd.Parameters( 2,1 ,i),sdd.Parameters( other_port,other_port ,i) );
Attached is a presentation that derives the formula on line 63, starting from the renormalization of a 2×2 S-matrix. It leads to an _expression_ for the renormalized return loss in terms of the original (unrenormalized)
S-parameters and the input/output reference impedances.
Regards,
Hansel D'Silva
From: Norman Swenson <norm.swenson@xxxxxxxx>
Sent: Saturday, July 19, 2025 11:10 AM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx <STDS-802-3-COM@xxxxxxxxxxxxxxxxx>
Subject: Re: [802.3_COM] Correction: Question about equation in function get_TDR
CAUTION: EXTERNAL EMAIL
Correction: The name of the function (and corresponding .m file) is get_TDR.
From: norm.swenson@xxxxxxxx <norm.swenson@xxxxxxxx>
Sent: Friday, July 18, 2025 10:30 PM
To: STDS-802-3-COM@xxxxxxxxxxxxxxxxx
Subject: Question about equation in function TDR_results
Hello all
I am trying to reverse engineer the current version of COM in the main
branch. Lines 62 and 63 of the function get_TDR define a pure function:
% re-normalize reference of s-parameterss: this seems correct for a s4p
input file [sic]
TDR_RL
=@(Zin,Zout,s11,s12,s21,s22)(Zin.^2.*s11+Zin.^2.*s22+Zout.^2.*s11+Zout.^2.*s
22+Zin.^2-Zout.^2
<mailto:=@(Zin,Zout,s11,s12,s21,s22)(Zin.%5e2.*s11+Zin.%5e2.*s22+Zout.%5e2.*
s11+Zout.%5e2.*s22+Zin.%5e2-Zout.%5e2> +
Zin.*Zout.*s11.*2.0-Zin.*Zout.*s22.*2.0+Zin.^2.*s11.*s22-Zin.^2.*s12.*s21-Zo
ut.^2.*s11.*s22+Zout.^2.*s12.*s21)./(Zin.*Zout.*2.0+Zin.^2.*s11+Zin.^2.*s22-
Zout.^2.*s11-Zout.^2.*s22+Zin.^2+Zout.^2+Zin.^2.*s11.*s22-Zin.^2.*s12.*s21+Z
out.^2.*s11.*s22-Zout.^2.*s12.*s21-Zin.*Zout.*s11.*s22.*2.0+Zin.*Zout.*s12.*
s21.*2.0);
In typeset form, TDR_RL is given by :
Or, expressing the numerator and denominator as polynomials in Zin and Zout,
TDR_RL is:
I am wondering what this is. Is this an _expression_ of the return loss when
Zin and Zout are the source and load impedances, respectively, when they
differ from the reference impedance Z0 used to calculate the s-parameters?
(If so, this would be along the lines of the presentation I made last Monday
to the interim working group meeting, but I would like to be sure.)
Thanks for any guidance anyone can provide.
Regards,
Norm
________________________________________________________________________
To unsubscribe from the STDS-802-3-COM list, click the following link: https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1
________________________________________________________________________
THIS EMAIL ORIGINATED FROM AN EXTERNAL SOURCE (outside of Amphenol-TCS),
PLEASE USE CAUTION WHEN EVALUATING ITS CONTENTS.
This e-mail has been scanned by MCI Managed Email Content Service, using Skeptic(tm)
technology powered by MessageLabs. To report SPAM or other related email issues please
send an email to Postmaster@xxxxxxxxxxxxxxxx
________________________________________________________________________
To unsubscribe from the STDS-802-3-COM list, click the following link:
https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1
To unsubscribe from the STDS-802-3-COM list, click the following link:
https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1
To unsubscribe from the STDS-802-3-COM list, click the following link:
https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1
To unsubscribe from the STDS-802-3-COM list, click the following link:
https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1
To unsubscribe from the STDS-802-3-COM list, click the following link: https://listserv.ieee.org/cgi-bin/wa?SUBED1=STDS-802-3-COM&A=1